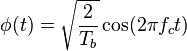BPSK

bpsk

BPSK (also sometimes called PRK, phase reversal keying, or 2 PSK) is the simplest form of phase shift keying (PSK). It uses two phases which are separated by 180° and so can also be termed 2-PSK. It does not particularly matter exactly where the constellation points are positioned, and in this figure they are shown on the real axis, at 0° and 180°. This modulation is the most robust of all the PSKs since it takes the highest level of noise or distortion to make the demodulator reach an incorrect decision. It is, however, only able to modulate at 1 bit/symbol (as seen in the figure) and so is unsuitable for high data-rate applications.

In the presence of an arbitrary phase-shift introduced by the communications channel, the demodulator is unable to tell which constellation point is which. As a result, the data is often differentially encoded prior to modulation.

bpsk

BPSK is functionally equivalent to 2-QAM modulation.

Implementation

The general form for BPSK follows the equation:

s_n(t) = \sqrt{\frac{2E_b}{T_b}} \cos(2 \pi f_c t + \pi(1-n )), n = 0,1.

This yields two phases, 0 and π. In the specific form, binary data is often conveyed with the following signals:

s_0(t) = \sqrt{\frac{2E_b}{T_b}} \cos(2 \pi f_c t + \pi ) = - \sqrt{\frac{2E_b}{T_b}} \cos(2 \pi f_c t)

for binary “0”

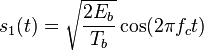s_1(t) = \sqrt{\frac{2E_b}{T_b}} \cos(2 \pi f_c t)

for binary “1”

where f_c is the frequency of the carrier-wave.

Hence, the signal-space can be represented by the single basis function

\phi(t) = \sqrt{\frac{2}{T_b}} \cos(2 \pi f_c t)

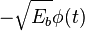where 1 is represented by $\sqrt{E_b} \phi(t)$ and 0 is represented by $-\sqrt{E_b} \phi(t)$ . This assignment is, of course, arbitrary.

This use of this basis function is shown at the end of the next section in a signal timing diagram. The topmost signal is a BPSK modulated cosine wave that the BPSK modulator would produce. The bit-stream that causes this output is shown above the signal (the other parts of this figure are relevant only to QPSK).