Addition and subtraction

The ALU is the core of the computer – it performs arithmetic and logic operations on data that not only realize the goals of various applications (e.g., scientific and engineering programs), but also manipulate addresses (e.g., pointer arithmetic). In this section, we will overview algorithms used for the basic arithmetic and logical operations. A key assumption is that twos complement representation will be employed, unless otherwise noted.

3.1.1. Boolean Addition

When adding two numbers, if the sum of the digits in a given position equals or exceeds the modulus, then a carry is propagated. For example, in Boolean addition, if two ones are added, the sum is obviously two (base 10), which exceeds the modulus of 2 for Boolean numbers (B = Z₂ = {0,1}, the integers modulo 2). Thus, we record a zero for the sum and propagate a carry valued at one into the next more significant digit, as shown in Figure 3.1.

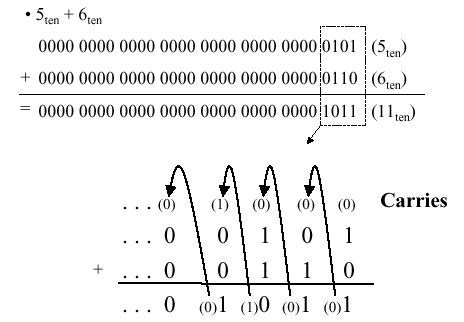
Figure 3.1. Example of Boolean addition with carry propagation, adapted from [Maf01].

3.1.2. Boolean Subtraction

When subtracting two numbers, two alternatives present themselves. First, one can formulate a subtraction algorithm, which is distinct from addition. Second, one can negate the subtrahend (i.e., in a – b, the subtrahend is b) then perform addition. Since we already know how to perform addition as well as twos complement negation, the second alternative is more practical. Figure 3.2 illustrates both processes, using the decimal subtraction 12 – 5 = 7 as an example.

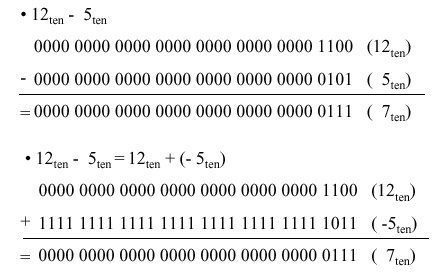
Figure 3.2. Example of Boolean subtraction using (a) unsigned binary representation, and (b) addition with twos complement negation – adapted from [Maf01].

Just as we have a carry in addition, the subtraction of Boolean numbers uses a borrow. For example, in Figure 3.2a, in the first (least significant) digit position, the difference 0 – 1 in the one’s place is realized by borrowing a one from the two’s place (next more significant digit). The borrow is propagated upward (toward the most significant digit) until it is zeroed (i.e., until we encounter a difference of 1 – 0).

3.1.3. Overflow

Overflow occurs when there are insufficient bits in a binary number representation to portray the result of an arithmetic operation. Overflow occurs because computer arithmetic is not closed with respect to addition, subtraction, multiplication, or division. Overflow cannot occur in addition (subtraction), if the operands have different (resp. identical) signs.

To detect and compensate for overflow, one needs n+1 bits if an n-bit number representation is employed. For example, in 32-bit arithmetic, 33 bits are required to detect or compensate for overflow. This can be implemented in addition (subtraction) by letting a carry (borrow) occur into (from) the sign bit. To make a pictorial example of convenient size, Figure 3.3 illustrates the four possible sign combinations of differencing 7 and 6 using a number representation that is four bits long (i.e., can represent integers in the interval [-8,7]).

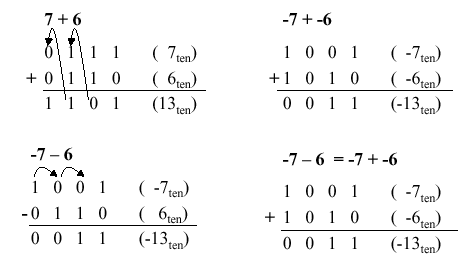
Figure 3.3. Example of overflow in Boolean arithmetic, adapted from [Maf01].

3.1.4. MIPS Overflow Handling

MIPS raises an exception when overflow occurs. Exceptions (or interrupts) act like procedure calls. The register $epc stores the address of the instruction that caused the interrupt, and the instruction

mfc register, $epc

moves the contents of $epc to register. For example, register could be $t1. This is an efficient approach, since no conditional branch is needed to test for overflow.

Two’s complement arithmetic operations (add, addi, and sub instructions) raise exceptions on overflow. In contrast, unsigned arithmetic (addu and addiu) instructions do not raise an exception on overflow, since they are used for arithmetic operations on addresses (recall our discussion of pointer arithmetic in Section 2.6). In terms of high-level languages, C ignores overflows (always usesaddu, addiu, and subu), while FORTRAN uses the appropriate instruction to detect overflow. Figure 3.4 illustrates the use of conditional branch on overflow for signed and unsigned addition operations.

Figure 3.4. Example of overflow in Boolean arithmetic, adapted from [Maf01].